9. Number Systems in Computer Science
This is a short and practical introduction into number systems in computer science generated with AI.
9.1 Different Number Systems
Imagine you're debugging a program that crashes mysteriously. The error message shows: Segmentation fault at address 0x7FFF5FBFF8A0. Or you're working with colors in web design and see #FF6B35. Why aren't these just normal decimal numbers?
The answer lies in how computers fundamentally work. Computers are binary machines - they only understand electrical states: ON (1) or OFF (0). Everything else is built on top of this foundation. Different number systems solve different problems:
- Binary: Matches how hardware actually works
- Hexadecimal: Provides a compact, human-readable way to view binary data
- Signed representations: Handle negative numbers efficiently
- Bit operations: Enable fast calculations and memory manipulation
Let's explore each system and understand not just what they are, but why we use them and how to work with them effectively.
9.2 Binary System (Base 2)

Computers use transistors. A transistor is a semiconductor device used to amplify or switch electronic signals and electrical power. It is one of the fundamental building blocks of modern electronic devices. A transistor can be either ON or OFF. This natural two-state system maps perfectly to binary digits (bits). Every piece of data in your computer - text, images, videos, programs - is ultimately stored as sequences of 0s and 1s.
Binary is a number system that uses only two digits: 0 and 1. While our everyday decimal system uses ten digits (0-9), binary works with just these two.
Think of binary like having a set of chips, where each chip has a specific value: 1, 2, 4, 8, 16, 32, 64, 128... (each chip is worth double the previous one).
For any number, you decide: Do I take this chip or not? - Take it = 1 - Don't take it = 0
Example: Convert 31 to binary
Available chips: 64, 32, 16, 8, 4, 2, 1
- 32? No, too big (31 < 32) → 0
- 16? Yes! (31 ≥ 16) → 1 | Remaining: 31 - 16 = 15
- 8? Yes! (15 ≥ 8) → 1 | Remaining: 15 - 8 = 7
- 4? Yes! (7 ≥ 4) → 1 | Remaining: 7 - 4 = 3
- 2? Yes! (3 ≥ 2) → 1 | Remaining: 3 - 2 = 1
- 1? Yes! (1 ≥ 1) → 1 | Remaining: 1 - 1 = 0
Result: 31 = 011111₂ (or simply 11111₂).
Example: Convert 1011₂ to decimal
Write down the chip values and add up the ones you "take" (where there's a 1):
Position: 8 4 2 1
Binary: 1 0 1 1
Take chips: 8 + 2 + 1 = 11
Result: 1011₂ = 11
In practice, binary numbers are grouped into fixed sizes: 8 bits (= 1 Byte), 32 bits, or 64 bits. The table below shows the values for an 8-bit number:
Position: 7 6 5 4 3 2 1 0
Power: 2⁷ 2⁶ 2⁵ 2⁴ 2³ 2² 2¹ 2⁰
Value: 128 64 32 16 8 4 2 1
finite
The Fundamental Limitation: Finite Bits = Finite Numbers
In mathematics, we can conceptually work with infinite numbers. On a traditional number line, we can always go further in either direction. However, computers use a fixed number of bits to represent numbers. This creates a fundamental constraint: with n bits, we can only represent 2ⁿ distinct values.
Examples:
- 3 bits → 2³ = 8 possible values
- 4 bits → 2⁴ = 16 possible values
- 8 bits → 2⁸ = 256 possible values
This limitation forces us to work within a bounded number space rather than the infinite mathematical number line.
With 4 bits, we can only represent values 0 through 15:
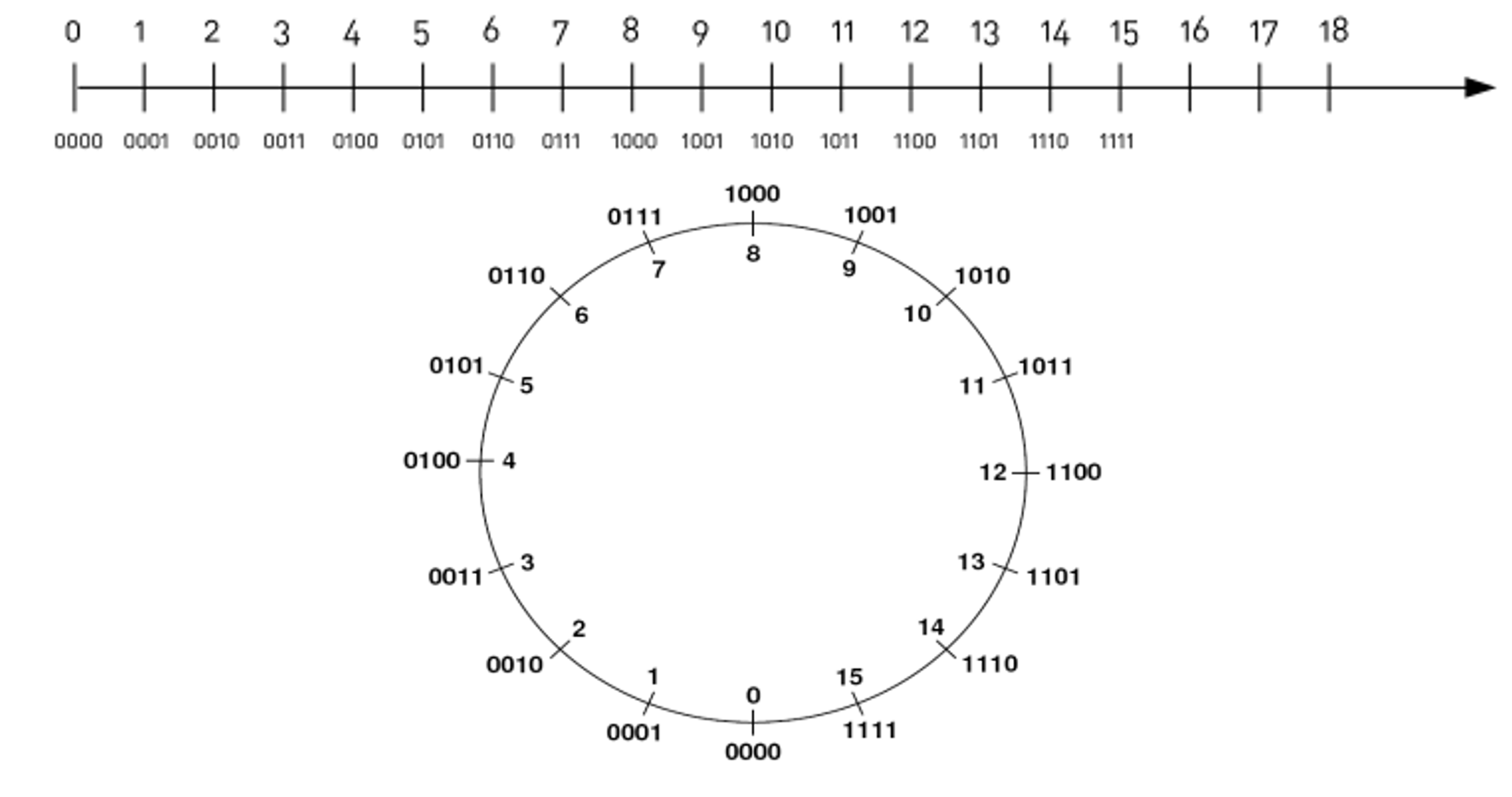
learn powers of 2 by heart
Learn the powers of 2 by heart: 2⁰=1, 2¹=2, 2²=4, 2³=8, 2⁴=16, 2⁵=32, 2⁶=64, 2⁷=128, 2⁸=256, 2⁹=512, 2¹⁰=1024
You can perform calculations with binary numbers just like with decimal numbers. The rules for addition are similar, but they follow base 2 instead of base 10.
Let's add two 4-bit binary numbers:
0110 (6 in decimal)
+ 0101 (5 in decimal)
-------
1011 (11 in decimal)
Adding a number means rotating clockwise around the circle. Subtracting a number means rotating counter-clockwise around the circle.
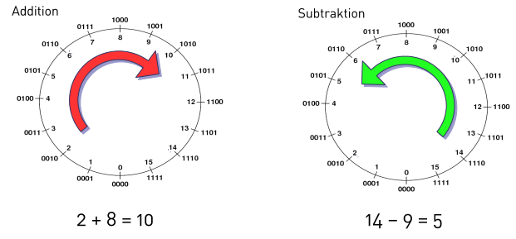
This circular representation shows why 15 + 1 = 0 in 4-bit arithmetic - we've wrapped around the circle!
9.2.1 kB, MB, ...
The size of a file refers to the number of bytes in that file. The following abbreviations are common
- kilobyte (kB) = 1.024 Byte
- Megabyte (MB) = 1.048.576 Byte
- Gigabyte (GB) = 1.073.741.824 Byte
- Terabyte (TB) = 1.099.511.627.776 Byte
9.3 Hexadecimal System (Base 16)
Binary is accurate but unwieldy. Try memorizing 11111111101101110011101000111010. Hexadecimal solves this by grouping 4 binary digits into one hex digit, making long binary numbers much more manageable.
The Hex Digits
Decimal: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Hex: 0 1 2 3 4 5 6 7 8 9 A B C D E F
Binary: 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111
Common Hex Values to Memorize:
- FF₁₆ = 255₁₀ (maximum 8-bit value)
- 100₁₆ = 256₁₀ (2⁸)
- 400₁₆ = 1024₁₀ (2¹⁰, 1 KB)
- 1000₁₆ = 4096₁₀ (2¹², common page size)
You can do arithmetic with hexadecimal numbers just like with decimal or binary numbers.
3A (58 in decimal)
+ 21 (33 in decimal)
-----
5B (91 in decimal)
9.3.1 Real-World Applications
- Memory Addresses:
0x7FFF5FBFF8A0- The0xprefix indicates hexadecimal - Each hex digit represents exactly 4 bits - Much easier to read than 64 binary digits! - RGB Colors**:
#FF6B35- FF = 255 (red channel, maximum intensity) - 6B = 107 (green channel, medium-low intensity)
- 35 = 53 (blue channel, low intensity) - Result: A vibrant orange color - Check the rgb color wheel - MAC Addresses**:
00:1B:44:11:3A:B7- Each pair represents one byte (8 bits) - Used to identify network devices uniquely
9.3.2 Conversion
Binary ↔ Hex Conversion: This is the easiest conversion because of the 4:1 relationship.
Binary to Hex: Group by 4 bits
Binary: 1101 1010 1100 0011
Hex: D A C 3
Result: DAC3₁₆
Hex to Binary: Each hex digit becomes 4 bits
Hex: 2F8A
Binary: 0010 1111 1000 1010
9.4 One's Complement
How do you represent -5 in binary? You can't just add a minus sign - computers only understand 0s and 1s. Early computer designers tried different approaches.
How One's Complement works: Simple rule: Flip every bit to make a number negative.
Example with 8-bit numbers:
+5 = 00000101₂
-5 = 11111010₂ (flip every bit)
The problem of this approach:
- Two representations of zero: +0 = 00000000, -0 = 11111111
- Arithmetic complications: Adding requires special handling
9.5 Two's Complement
Two's complement solves all the problems of one's complement:
- Only one representation of zero
- Addition and subtraction work with the same hardware
- Clean mathematical properties
Method: Flip all bits, then add 1
+5 = 00000101₂
Step 1: Flip bits → 11111010₂
Step 2: Add 1 → 11111011₂ = -5
Two's complement has a beautiful symmetry: if A is the two's complement of B, then B is the two's complement of A. This symmetry eliminates the need for separate "encoding" and "decoding" algorithms - the same process works in both directions, making two's complement both mathematically elegant and computationally efficient.
Converting Two's Complement Back to Decimal
- Check the sign bit (leftmost bit)
- If 0: positive number → convert directly to decimal
- If 1: negative number → apply two's complement operation, i.e.
- Flip all bits (0→1, 1→0)
- Add 1
- The result gives you the magnitude
- Add minus sign
Examples
0101₂(4-bit)- Sign bit = 0 → positive
- Direct conversion: 0×8 + 1×4 + 0×2 + 1×1 = 5
1011₂(4-bit)- Sign bit = 1 → negative
- Flip bits:
1011→0100 - Add 1:
0100 + 1=0101 - Convert:
0101= 5 - Result: -5
9.6 Unsigned vs. Signed Representation
The same bit patterns can represent completely different number ranges depending on our interpretation:
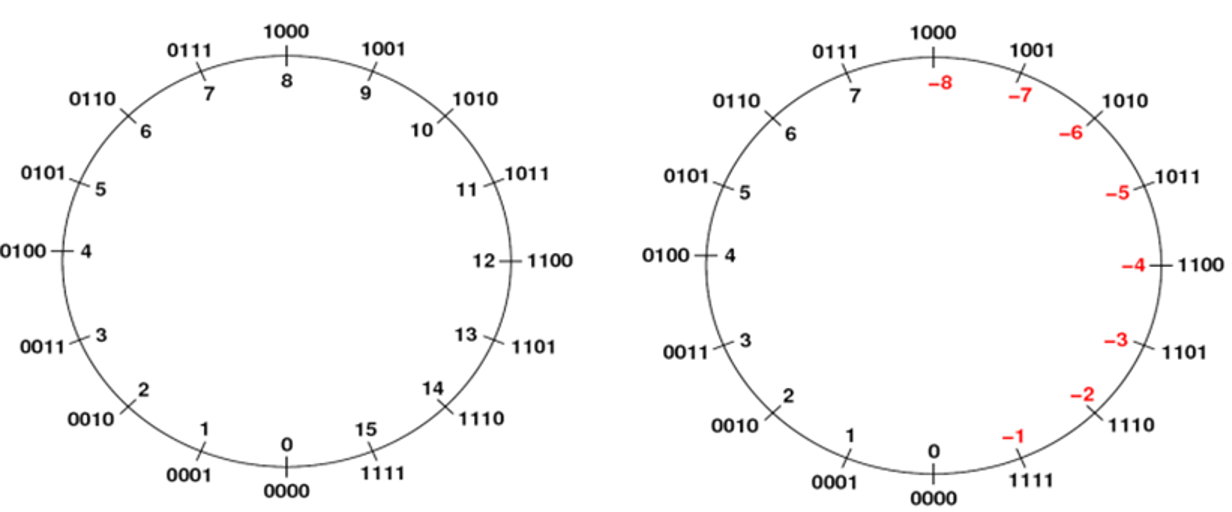
Programming Languages: Every signed integer type (int, long, short) uses two's complement
int x = -1; // Internally: 11111111111111111111111111111111 (32-bit)
Overflow Behavior: Understanding two's complement explains integer overflow
int x = 2147483647; // Maximum 32-bit signed integer
x = x + 1; // Result: -2147483648 (wraps around)
9.6.1 Number Range
- With n bits in two's complement
- Range: -2ⁿ⁻¹ to 2ⁿ⁻¹ - 1
- 8-bit: -128 to +127
- 32-bit: Standard integers in most languages
- Unsigned Integer Ranges with n bits
- Range: 0 to 2ⁿ - 1
- 8-bit: 0 to +255
- RGB color values, ASCII characters
9.7 Bit Shifting
Division and multiplication are expensive operations for processors. In performance-critical code (games, embedded systems, real-time processing), every microsecond counts. Bit shifting provides a lightning-fast alternative for powers of 2.
Left Shift (<<): Multiplication by Powers of 2 - Each left shift multiplies by 2
5₁₀ = 00000101₂
5 << 1 = 00001010₂ = 10₁₀ (5 × 2¹)
5 << 2 = 00010100₂ = 20₁₀ (5 × 2²)
5 << 3 = 00101000₂ = 40₁₀ (5 × 2³)
Formula: x << n equals x × 2ⁿ
Right Shift (>>): Division by Powers of 2 - Each right shift divides by 2 (integer division)
40₁₀ = 00101000₂
40 >> 1 = 00010100₂ = 20₁₀ (40 ÷ 2¹)
40 >> 2 = 00001010₂ = 10₁₀ (40 ÷ 2²)
40 >> 3 = 00000101₂ = 5₁₀ (40 ÷ 2³)
Formula: x >> n equals x ÷ 2ⁿ (rounded down)
9.8 IEEE 754 Floating-Point Format
You've probably encountered this mysterious behavior:
#include <iostream>
using namespace std;
int main() {
cout << (0.1 + 0.2) << endl; // Output: 0.3
cout << (0.1 + 0.2 == 0.3) << endl; // Output: 0 (false)
return 0;
}
Or perhaps you've wondered why your financial calculation went wrong:
double price = 0.10;
double tax = 0.02;
double total = price + tax; // Should be 0.12, but might be 0.12000000000000001
Or
float x= 1.0e20f,
y = 1.0f,
z = 1.0e20f,
u = 1.0f;
std::cout << y/((x+y-z)*u); // should be 1 but gives inf
These aren't bugs - they're fundamental limitations of how computers represent decimal numbers. Unlike integers, which can be represented exactly in binary, most decimal fractions cannot be represented exactly in binary, just as 1/3 cannot be represented exactly in decimal (0.333...).
The IEEE 754 standard was created to solve several critical problems:
- Standardization: Before IEEE 754, every computer manufacturer had their own floating-point format, making programs non-portable
- Range vs. Precision Trade-off: How to represent both very large numbers (like the distance to stars) and very small numbers (like atomic measurements) in limited bits
- Special Values: How to handle division by zero, square roots of negative numbers, and other mathematical edge cases
- Predictable Behavior: Ensuring that the same calculation produces the same result on different computers
Before diving into IEEE 754, let's understand scientific notation, which forms the basis of floating-point representation.
Decimal Scientific Notation: significand × 10^exponent
- 1 234 = 1.234 × 10³
- 0.00567 = 5.67 × 10⁻³
The same principle applies in binary: significand × 2^exponent
- 12.75₁₀ = 1100.11₂ = 1.10011₂ × 2³
- 0.375₁₀ = 0.011₂ = 1.1₂ × 2⁻²
Just as whole numbers use positive powers of 2 to the left of the decimal point, fractions use negative powers of 2 to the right:
... 2³ 2² 2¹ 2⁰ . 2⁻¹ 2⁻² 2⁻³ 2⁻⁴ ...
... 8 4 2 1 . 1/2 1/4 1/8 1/16 ...
... 8 4 2 1 . 0.5 0.25 0.125 0.0625 ...
Example: 0.75₁₀ in Binary
0.75 = 3/4 = 1/2 + 1/4
Position: 2⁰ . 2⁻¹ 2⁻²
Value: 1 . 1/2 1/4
Binary: 0 . 1 1
So 0.75₁₀ = 0.11₂
9.8.1 Normalization
In binary, we can always adjust the exponent so the significand starts with 1. This is called normalized form:
- 1100.11₂ = 1.10011₂ × 2³ (normalized)
- 0.110011₂ = 1.10011₂ × 2⁻¹ (normalized)
Since the first digit is always 1, we don't need to store it! This gives us an extra bit of precision - the implicit leading bit.
IEEE 754 represents floating-point numbers using three fields:
[Sign][Exponent][Fraction/Mantissa]
- Sign Bit (S): 0 = positive, 1 = negative
- Exponent (E): Stored with a bias for easier comparison
- Fraction/Mantissa (F): The fractional part after the implicit leading 1
Single Precision (32-bit) Layout
[S] [Exponent] [Fraction]
1 8 23
[S] [Exponent] [Fraction]
1 11 52
9.8.2 Bias
In IEEE 754, a bias is added to the exponent to simplify comparisons. This bias is:
- 127 (2⁷ - 1) for single precision
- 1023 (2¹⁰ - 1) for double precision
For example
- An exponent of +3 is stored as 3 + 127 = 130, which is 10000010 in binary.
- An exponent of -1 is stored as -1 + 127 = 126, which is 01111110 in binary.
Thus, the binary comparison 10000010 > 01111110 correctly reflects that +3 > -1. In two's complement representation, negative numbers have a leading 1, making direct binary comparisons more complex because the sign bit must be considered separately.
9.8.3 Conversion Process

Example 1: Converting 12.75₁₀ to Single Precision
Step 1: Convert to Binary
12₁₀ = 1100₂
0.75₁₀ = 0.11₂ (3/4 = 1/2 + 1/4)
12.75₁₀ = 1100.11₂
Step 2: Normalize
1100.11₂ = 1.10011₂ × 2³
Step 3: Extract Components
- Sign: Positive → S = 0
- Exponent: 3 → Biased = 3 + 127 = 130 = 10000010₂
- Fraction: .10011 → Pad with zeros → 10011000000000000000000₂
Step 4: Assemble
Sign: 0
Exponent: 10000010
Fraction: 10011000000000000000000
Result: 01000001010011000000000000000000₂

Example 2: Converting Single Precision 01000001010011000000000000000000 to decimal
-
Extract the components
- Sign bit:
0(positive number) - Exponent:
10000010 - Significand:
10011000000000000000000
- Sign bit:
-
Convert the exponent
- The exponent is stored with a bias of 127. So, subtract 127 from the exponent value.
10000010in binary is130in decimal.130 - 127 = 3
-
Convert the significand
- The significand has an implicit leading 1, so we prepend a 1 to the significand:
1.10011 - Convert the fractional part to decimal:
1 + 1/2 +1/16 + 1/32
- The significand has an implicit leading 1, so we prepend a 1 to the significand:
- Combine the components
- The decimal value is calculated as:
s*m*2^exponent (1 + 1/2 +1/16 + 1/32) × 2³ = 8 + 4 + 0.5 + 0.25 = 12.75
- The decimal value is calculated as:
9.8.4 Best Practices
- Choose appropriate precision based on your accuracy requirements
- Avoid direct equality comparisons - always use epsilon tolerance
- Be aware of cancellation errors in subtraction of similar values
- Handle special values (NaN, infinity) explicitly
Understanding IEEE 754 is crucial for any programmer working with real numbers. It explains why floating-point arithmetic behaves the way it does and helps you write more robust, predictable code. Remember: floating-point numbers are approximations, not exact values, and designing with this limitation in mind will save you from mysterious bugs and incorrect results.
check
Use the IEEE-754 Konverter to check your calculation.
