9. Encoding, Compression & Data Representation

Imagine you're building a messaging app. Users want to send text in different languages, emojis, images, and videos. But computers only understand binary numbers (0s and 1s). How do you bridge this gap?

Or consider Netflix streaming a 4K movie to millions of users simultaneously. A single 2-hour 4K movie without compression would be about 7 terabytes - impossible to stream over the internet. Yet you can watch it smoothly on your phone with just a few megabytes per second.

These challenges led to three fundamental concepts that power our digital world:

1. Encoding: How to represent different types of information as binary numbers
2. Compression: How to make data smaller while preserving its essential information
3. Encryption: How to hide information from unauthorized access (briefly covered -- more in the module IT Security)

Let's explore how each solves different problems and why understanding them is crucial for modern computing.

9.1 Character Encoding: From ASCII to Unicode

In the early days of computing, ASCII (American Standard Code for Information Interchange) seemed sufficient:

// ASCII encoding (7-bit, 128 characters)
'A' = 65  = 01000001₂
'a' = 97  = 01100001₂  
'0' = 48  = 00110000₂
' ' = 32  = 00100000₂

9.1.1 Unicode: The Universal Solution

Unicode aims to represent every character ever used by humans

• Over 144,000 characters defined
• Covers 159 modern and historical scripts
• Includes emojis, mathematical symbols, and even €

9.1.2 UTF-8

UTF-8 is variable-length encoding - it uses 1-4 bytes per character:

// UTF-8 examples
'A'  → 01000001₂                    (1 byte, ASCII compatible)
'é'  → 11000011 10101001₂           (2 bytes)
'😀' → 11110000 10011111 10011000 10000000₂ (4 bytes)

9.2 Linear Codes

Every time you send a message or store a file, there's a chance that some bits get corrupted. Linear codes help detect and fix such errors, ensuring that the original information can be reconstructed.

9.2.1 Vectors and Vector Spaces

A vector is simply a list of numbers. In binary coding, vectors are made of 0s and 1s. Example: (1, 0, 1) is a 3-dimensional binary vector.

You can also imagine vectors as points or arrows in space.

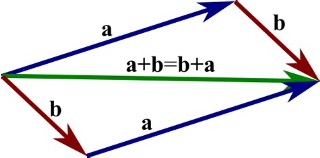
Adding vectors means combining directions. This can be visualized as forming the diagonal of a rectangle — the sum vector.

A set of vectors is a vector space if:

• You can add any two vectors, and the result is still in the set.
• You can multiply any vector by a number (just 0 or 1 in binary), and it stays in the set.

A linear code is simply a set of binary vectors that forms a vector space.

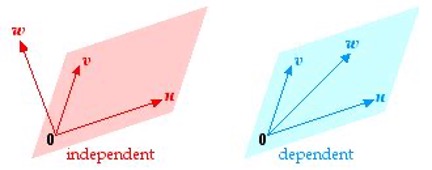
Vectors are linearly dependent if one can be written as a combination (XOR sum) of others.

Example (not linear):

C = {000, 011, 111, 110}
011 ⊕ 110 = 101 → not in C → ❌ not linear

Hamming Distance: Number of positions where two codewords differ.

Codeword 1: 1011001  
Codeword 2: 1110101  
Differences: ↑ ↑ ↑   → Distance = 3

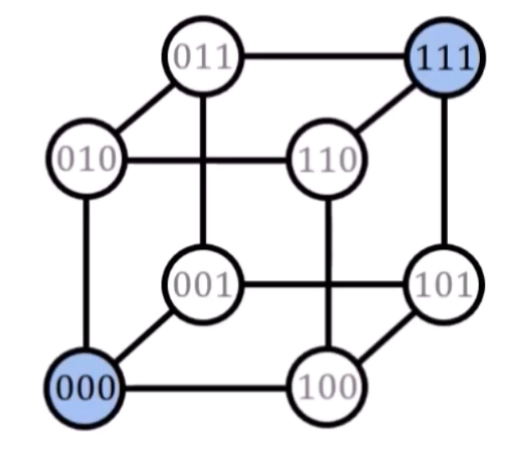
Given the code C = {(0,0,0), (1,1,1)}, the Hamming distance is 3. Any other 3-bit word — for example, (1,0,0) — is not part of the code.

Now suppose we send (0,0,0), but receive (1,0,0). Since (1,0,0) is not a valid codeword, we know an error has occurred.

We compare it to the valid codewords and find that (1,0,0) is closer (in Hamming distance) to (0,0,0) than to (1,1,1). So we assume that one bit was flipped, most likely the first one.

We then correct the error and recover the original codeword (0,0,0).

• Dependent vectors cluster closely in space → small Hamming distance

• Independent vectors are more spread out → large Hamming distance

Why does this matter? Because the more “spread out” your codewords are, the more errors you can detect and correct.

9.2.1.1 Common Linear Codes

• Hamming codes – Detect and correct single-bit errors. Used in RAM and storage.
• Reed–Muller codes – Stronger codes for noisy environments like deep-space or magnetic media.

9.3 Prefix-Free Codes

Suppose we want to encode characters using binary:

A = 1  
B = 10  
C = 11

Now, given the string 110, how do we decode it?

• 1 + 10 → "AB"?
• 11 + 0 → "C" and ???
• We can't tell where one codeword ends and the next begins.

This kind of ambiguity makes reliable decoding impossible.

A prefix-free code is one where no codeword is the prefix of another. This ensures that decoding is immediate and unambiguous.

9.3.0.1 Example of a prefix-free code:

A = 0  
B = 10  
C = 110  
D = 111

Now every codeword can be uniquely decoded:

• 0 → A
• 10 → B
• 110 → C
• 111 → D

You never have to guess or backtrack — the decoder can process the stream bit by bit.

9.3.1 🌲 Visualizing Prefix-Free Codes as a Binary Tree

Prefix-free codes can be illustrated as a binary tree

        (root)
        /    \
     A(0)    (1)
            /   \
         B(10)  (11)
                /  \
             C(110) D(111)

How decoding works: Start at the root, read one bit at a time (0 = left, 1 = right), and stop when you reach a leaf. That’s your decoded symbol.

9.3.2 ☎️ Phone Numbers

Phone numbers are designed to be prefix-free — at least within a country or region.

For example, in Germany

030 — Berlin  
040 — Hamburg  
069 — Frankfurt

You’ll never have two valid area codes where one is a prefix of the other. Otherwise, dialing would be ambiguous:

• If both 03 and 030 existed, how would the system know when to stop reading the area code?

Prefix-free numbering ensures that the system knows when the area code ends and the subscriber number begins — just like a decoder knows when a binary codeword ends.

9.3.3 Huffman Coding

In most texts, some letters occur far more often than other. But in standard encodings like ASCII every character gets the same number of bits (e.g. 8 bits each). That’s wasteful — we’re spending too much space on common letters.

We can save space by using

• Shorter codes for frequent characters
• Longer codes for rare characters

Huffman coding does exactly that — and guarantees the most efficient prefix-free code possible for a given set of symbol frequencies.

🛠️ How Huffman’s Algorithm Works

1. Count how often each symbol appears
2. Create leaf nodes for each symbol
3. Build a binary tree, combining the two least frequent nodes step by step
4. Assign binary codes: left edge = 0, right edge = 1

Example: "ABACABAD"

Frequencies:
A: 4  
B: 2  
C: 1  
D: 1

• Combine C(1) + D(1) → CD(2)

Frequencies:    Tree:    CD
A: 4                    /  \
B: 2                   C    D
CD: 2  

Frequencies:    Tree:  BCD 
A: 4                   /  \
BCD: 4                B   CD    
                         /  \
                        C    D 

       Root
       / \
      A  BCD  
        /  \
       B   CD    
          /  \
         C    D 

• A = 0
• B = 10
• C = 110
• D = 111

Encoding "ABACABAD":

A  B  A  C  A  B  A  D  
0 10  0 110 0 10  0 111  → 14 bits total

Compare to ASCII: 8 characters × 8 bits = 64 bits.

However, Huffman codes are not fixed (they depend on the input data), the decoder needs to know the exact tree used during encoding. Hence, we need to transmit the tree with the data

• The Huffman tree or code table is included at the beginning of the encoded file.
• This is typical for compressed files like ZIP or PNG.
• The tree is usually stored in a compact form (e.g. a list of symbols and their bit-lengths).

Huffman encoding is a core tool in lossless data compression — whenever exact recovery is essential.

9.4 JPEG Compression

Now that we’ve seen how Huffman coding reduces data size by assigning short codes to common values, let’s look at how JPEG uses it as the final step in compressing images. JPEG goes further: it uses our eyes’ weaknesses and clever math to throw away detail we won’t miss — and then Huffman-codes the rest.

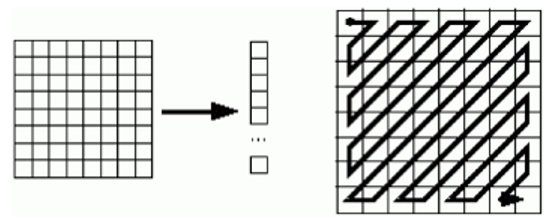
1. Linearization The image is split into small 8×8 blocks of pixels — like tiny tiles. Each block is processed separately.

2. Color Conversion The RGB color channels are transformed into brightness (Y) and color differences (Cb, Cr). Our eyes care more about brightness, so color can be stored more coarsely.

3. Cosine Transformation Each 8×8 block is converted into a mix of patterns — like checkerboards and stripes. This tells us how much fine detail is in the block, rather than storing every pixel directly.

4. Quantization Tiny details (high frequencies) are rounded off or dropped — especially from color. This is where JPEG loses quality, but in a smart, mostly invisible way.

5. Huffman Coding The remaining numbers are mostly small or zero. These are encoded efficiently using Huffman codes, like we learned before.

9.5 🎥 Video Compression

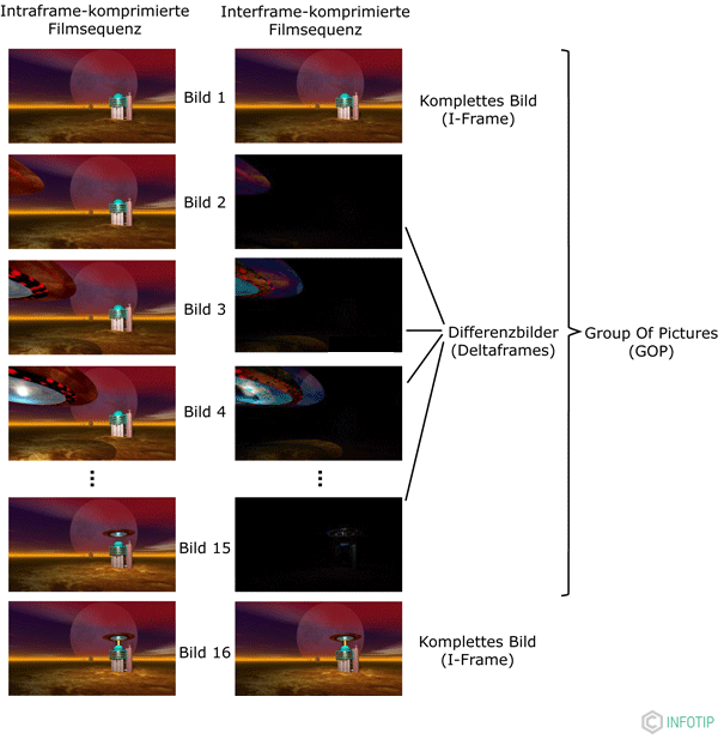
Clearly, storing or streaming video without compression is impossible for most real-world applications.

Most video frames are very similar — only small parts change (like a person moving).

Instead of storing every single frame as a full image, video compression uses differences between frames to save space.

• I-frame (Intra frame): A full image — like a JPEG. It's the starting point.
• Delta frames (P-frames or B-frames): Only store what's changed since the last frame (like motion). Much smaller!

To organize this, videos are split into GOPs (Groups of Pictures), like:

I   P   P   P   I   P   P   P   ...
↑                   ↑
Full frame        Full frame

This makes video much smaller — often over 100× smaller — with little visible difference.